Pistol sights

There are some things about handgun sights which I’ve never seen explained properly – that is to say, so that even someone without any gun experience can look at the explanation and check that it is correct, rather than having to take something on faith. Yet they do have reasonably simple explanations.

One of these is the dictum to always focus on the front sight. This is in regard to “iron sights”, the usual type, which most often feature a post as the front sight and a notch as the rear sight; you align the sights by putting the post in the middle of the notch, and put the target right in the middle of the post, as shown below (rear sight in gray, front in black, and the target is the red X):

Or at least that’s the nominal sight picture. But of course really you can only focus at one distance, so at least two out of those three things have to be out of focus. Focusing on the middle one (the front sight) should yield the best overall results, and that’s always been a good enough explanation to satisfy me personally, but for expository purposes I’ll calculate exactly what this looks like.

To pick a reasonably representative set of numbers, let’s say the rear sight is 300mm away from your eye, the front sight is another 150mm away, and the target is 5 meters away. And say the front sight post is 3mm wide and the rest of the image is to scale. And suppose your eye pupil is opened to 4mm diameter. (That last number might be twice as large in the dimmest of light or half as large in bright light; and the blurriness from being out of focus scales in direct proportion to it. So if you’re shooting in full daylight, you might have only half as much blurriness as shown in the following images. But your enemies may not do you the courtesy of attacking in full daylight.)

If you focused on the target, the 4mm of pupil diameter yields almost the full 4mm of blurriness diameter for both the sights: 3.76mm at the rear and 3.64mm at the front. With this image, the 3mm width of the front sight is 37 pixels, so 3.64mm of blurring is 45 pixels’ worth. The rear sight is closer, so a pixel translates to fewer millimeters: one pixel equates not to 3/37 mm but to (3/37) * (300/450) mm. So its blurring diameter is 70 pixels.

Now, lots of graphics packages offer a “Gaussian blur” feature, but that’s not what we want here; it would look sort of vaguely correct, but really out-of-focus blur is not a convolution with a Gaussian, aka Gaussian blur; instead it’s a convolution with a sharply-defined circle. (To illustrate this, if you take a point source of light and focus it onto a wall with a magnifying glass, then move it a bit out of focus, what you’ll see is an evenly-illuminated circle, not a Gaussian pattern of illumination, which would be a “bell curve” with the highest intensity in the middle, fading to the outsides.)

Performing those convolutions (this time with the rear sight being fully black), we get this sight picture:

So if you focus on the target, the sights are almost completely blurred out. Looking at the above picture, one might think it was still somewhat possible to aim using them, but a red X on a pure white background is close to the best possible scenario; practical scenarios involve much less contrast and more variation in the background.

Alternatively, if you focus on the rear sight, the front sight gets 2mm of blur (25 pixels), and the target gets 63mm (70 pixels), the result being:

This time it’s the target’s turn to get blurred out.

Now for the recommended focus on the front sight. This gives 1.3mm of blur on the rear sight (11 pixels), and 40mm (45 pixels) on the target:

This is obviously the winner, though the target is still pretty blurry. Of course it’s still inferior to optical sights, where you focus on the target and the crosshairs or red dot are superimposed optically and in perfect focus. But optical sights small and robust enough to be mounted on a pistol slide are a recent development, and are costly; very few handguns have one mounted. Laser sights, which project a laser beam onto the target, offer the same freedom to focus on the target, plus the freedom to actually see the whole target rather than having it blocked by the view of your gun. They are cheaper and more widely used. But if it’s dark, the laser gives away your position; and if it’s bright daylight, the laser has a very limited useful range.

There is another advantage, too, of laser and optical sights, which I have not seen remarked on much, but which is huge. With iron sights, you have two things to align: the front sight with the rear sight, and the front sight with the target. With optical or laser sights, you have only one: the reticle with the target. This is not just half the difficulty; it is much less than half, since with iron sights both alignments have to be accomplished at the same time. Now, if you really were super-adept with iron sights, you might recognize that this sight picture:

and this one:

actually represent shots that will land dead center on the target, since in both cases the error in front-sight to rear-sight alignment cancels out the error in front-sight to target alignment. But calculating this is not to be expected from anything like an ordinary handgun user – who, if he needs the accuracy, must correct both errors rather than calculating that they cancel.

But to return to the case of iron sights, which still are the only sort of sight mounted on probably upwards of 99% of the handguns in existence in the world, the fact that both alignments need to be performed doesn’t mean they are equally important. They aren’t: the front-sight to rear-sight alignment is more important than the front-sight to target alignment. For instance, with the above numbers for sight distances it is twice as important: a given angle of deviation from alignment between front and rear sights produces twice the error that as is produced by the same angle of deviation between front sight and the target. (“Angle”, here, refers to the angle as perceived by the eye, and “error” is the error in the angle of departure of the bullet.) How this comes about is shown in this diagram:

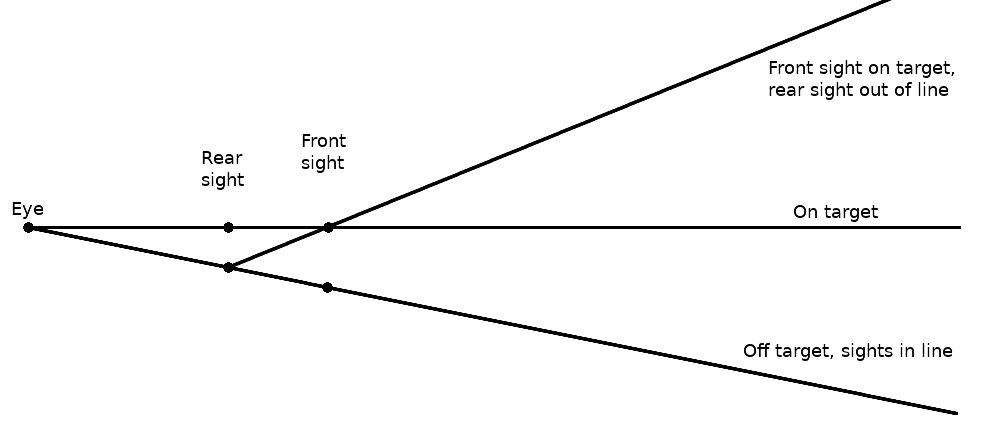
The factor of two in importance comes directly from the ratio of the distance from the eye to the rear sight to the distance from the rear sight to the front sight, which by the numbers I used is also a factor of two (300mm vs 150mm). Two is a reasonable ballpark number for a full-size pistol held with a normal two-handed hold by an average-size adult, but with a snubnose revolver it might be four or more. Or in the other direction, an unusual hold that brings a handgun close to the face can reduce the number.

Here’s what the factor of two looks like from behind the sights. This is the case of sights lined up but pointing in the wrong direction (impact point superimposed in yellow):

and this is the unaligned sights case:

I was told once by a proficient pistol shooter that he ignored where the front sight was on the target, and paid attention only to the alignment of the two sights relative to each other. Since he did in fact hit the target, and quite accurately too, he couldn’t have been entirely ignoring it; at the time, I filed his comment under “mysterious things people say”, but now I realize that what he was trying to get at was this difference in importance: the alignment of the front sight with the target was so much less important that he could relegate it to a background task in his brain and spend all his active concentration on the alignment of the two sights.

People also are referring to this difference in importance when they speak of the “sight radius” of a weapon (the distance between the two sights) and of a short sight radius making it hard to aim, but I don’t think I’ve ever seen anyone explain exactly why, or mention that when one does have to deal with a short sight radius, a partial remedy is to concentrate more attention on the alignment of the two sights.

So clearly this difference in importance is something that is known on some level, or at least used to be, though it is so seldom explained that I had to figure it out myself.

(A Russian translation of this article by Vlad Brown can be found here, a Ukrainian translation by Sandi Wolfe can be found here, and an Uzbek translation by Fedor Mironov can be found here.)